用Excel方差公式计算数据的离散程度（掌握Excel方差公式）

在统计学和数据分析领域，方差是衡量数据分布离散程度的重要指标之一。而在使用Excel进行数据处理和分析时，掌握方差的计算方法是非常实用的。本文将详细介绍如何使用Excel方差公式来计算数据的离散程度，帮助读者更好地理解和应用这一概念。

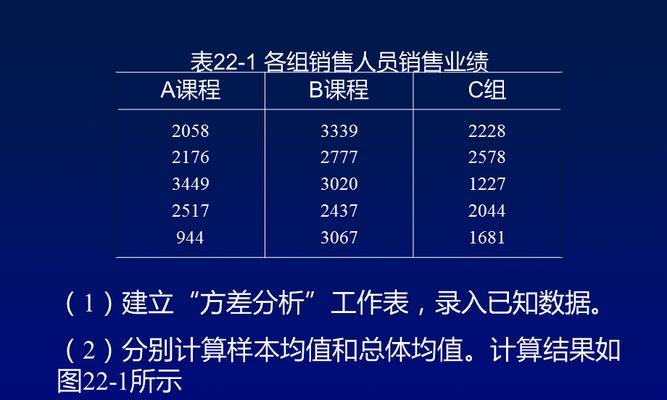
一：什么是方差

方差是用来衡量数据集中各个数据与其均值之间的偏离程度的统计指标。简单来说，方差越大表示数据集中的数据越分散，方差越小表示数据集中的数据越集中。

二：为什么要使用方差

方差能够帮助我们判断数据的离散程度，了解数据的分布情况。通过计算方差，我们可以更好地理解数据的变化情况，从而做出更准确的决策和预测。

三：Excel方差公式是什么

在Excel中，计算方差的公式是通过使用VAR函数来实现的。VAR函数可以计算一组数据的方差，并返回结果。

四：VAR函数的基本语法

在使用VAR函数时，需要将待计算方差的数据作为参数传入函数中。要计算A1到A10单元格中数据的方差，可以使用VAR(A1:A10)。

五：方差公式的步骤

使用VAR函数计算方差时，首先需要选择一个空白单元格作为输出结果的位置。在该单元格中输入VAR函数，并在括号内填入待计算方差的数据范围。

六：方差公式的参数设置

在填写VAR函数的括号内，可以选择性地添加一个或多个参数。这些参数用于指定方差计算的方式，如是否考虑样本误差等。默认情况下，VAR函数会假设输入的数据是样本数据。

七：使用方差公式计算离散程度

通过应用VAR函数，Excel会自动计算出数据集的方差，并将结果显示在选择的输出单元格中。方差的值越大，表示数据集的离散程度越高。

八：方差公式的应用场景

方差公式在实际数据分析中有广泛的应用。比如在投资领域，通过计算股票收益率的方差，可以评估投资组合的风险。

九：方差公式的局限性

方差公式在某些情况下可能存在一些局限性。方差无法判断数据集中是否存在异常值，也无法衡量数据分布的形状。

十：方差公式的相关函数

在Excel中，除了VAR函数之外，还有一些与方差计算相关的函数可供使用。VAR.S函数和VAR.P函数分别用于计算样本方差和总体方差。

十一：如何解决方差公式的问题

为了解决方差公式的局限性，我们可以结合其他统计方法和图表来更全面地分析数据的离散程度和分布情况。

十二：使用Excel其他工具进行数据分析

除了方差公式外，Excel还提供了一系列强大的数据分析工具，如直方图、散点图和回归分析等。这些工具可以帮助我们更深入地理解数据的特征和趋势。

十三：方差计算方法的重要性

通过本文对Excel方差公式的介绍，我们可以看到方差计算方法在统计学和数据分析中的重要性。掌握方差公式不仅可以帮助我们更好地理解数据的离散程度，还能为决策和预测提供有力的支持。

十四：Excel方差公式的使用方法

通过本文的介绍，我们了解到了如何使用Excel方差公式来计算数据的离散程度。使用VAR函数，并按照步骤填写参数，即可快速得到方差结果。

十五：展望方差公式在数据分析中的应用

方差公式作为数据分析的基础方法之一，在实际应用中有着广泛的应用前景。通过不断学习和应用方差公式，我们可以进一步提升数据分析的能力，并为更复杂的问题找到解决方案。

本文详细介绍了如何使用Excel方差公式来计算数据的离散程度。通过掌握方差的计算方法，读者可以更好地理解和应用这一概念，在数据分析和决策中发挥更大的作用。同时，本文也提到了方差公式的局限性，以及如何结合其他统计方法和工具来进一步分析数据的特征和趋势。通过不断学习和应用，我们可以不断提升数据分析能力，为实际问题提供准确和可靠的解决方案。

掌握Excel方差公式的使用方法

在使用Excel进行数据分析时，方差是一个常用的统计指标。它衡量了一组数据的离散程度，帮助我们了解数据的变化情况。本文将详细介绍如何使用Excel方差公式，帮助读者快速掌握方差计算的方法。

1.Excel中方差公式的基本概念

Excel中的方差公式用于计算一组数据的离散程度，即数据的变异程度。方差公式基于每个数据点与平均值之间的差异，可以帮助我们了解数据的分布情况。

2.方差公式的具体计算方法

在Excel中，使用VAR.S函数可以计算总体方差，而VAR.P函数用于计算样本方差。这两个函数接受一组数据作为参数，并返回对应的方差值。

3.使用Excel内置函数计算方差

在Excel中，我们可以直接使用内置的VAR.S和VAR.P函数来计算方差。只需要选中数据范围，然后在公式栏中输入对应函数即可得到方差值。

4.自定义方差公式的实现方法

如果需要自定义方差计算公式，可以使用Excel的SUM、AVERAGE等函数结合数学运算符来实现。通过自定义公式，可以满足特定需求，例如排除异常值或加权计算。

5.方差的常见应用场景

方差作为一种常用的统计指标，在各种数据分析场景中都有广泛的应用。比如在投资组合分析中，方差可以衡量不同资产之间的风险程度。

6.方差计算结果的解读与分析

方差计算得到的结果是一个非负数，其大小表示数据的离散程度。较小的方差意味着数据集中度较高，而较大的方差则表示数据分散程度较高。

7.Excel中方差公式的注意事项

在使用方差公式时，需要注意数据范围的选择，确保包含了所有需要计算方差的数据点。还需要留意使用VAR.S和VAR.P函数时的数据类型区别。

8.使用Excel图表可视化方差分析结果

通过在Excel中创建图表，我们可以直观地展示方差分析的结果。例如使用折线图或柱状图来比较不同数据集之间的方差差异。

9.方差公式在数据质量控制中的应用

在数据质量控制中，方差公式可以帮助我们判断数据集的一致性和稳定性。通过分析方差的变化情况，可以发现数据是否存在异常或波动。

10.方差与其他统计指标的关系

方差是一种常用的统计指标，但它并不能完全代表数据的整体特征。与均值、标准差等指标相比，方差更加关注数据的离散程度。

11.方差计算的案例分析

通过一个实际案例，我们可以深入理解方差的计算方法及其在数据分析中的作用。案例分析可以帮助读者更好地应用方差公式进行实际工作。

12.方差公式在预测模型评估中的应用

在构建预测模型时，方差公式可以作为评估模型准确性的指标之一。通过计算预测结果与实际值之间的方差，我们可以评估模型的稳定性和准确性。

13.方差计算在六西格玛管理中的应用

六西格玛管理方法中常使用方差计算来衡量过程稳定性和性能。通过分析方差，可以找出导致产品质量波动的原因，并采取相应措施进行改进。

14.Excel方差公式的高级应用

除了基本的方差计算，Excel还提供了一些高级函数和工具，如VARA、VARPA、数据分析工具等，可以帮助用户更加灵活地进行方差分析。

15.

通过本文的学习，我们掌握了在Excel中使用方差公式的方法，了解了方差的概念、计算方法以及应用场景。熟练掌握方差公式，可以帮助我们更好地进行数据分析和决策。